|
 |
Jean-Charles Faugère
Research Director/Senior Scientist at INRIA (Paris-Rocquencourt Research Center)
Head of the INRIA/UPMC POLSYS project team (former SALSA team).
Adresse Postale:
UFR Ingénierie 919
LIP6
Boite courrier 169
4, place Jussieu
F-75252 Paris Cedex 05
France |
Adresse:
Tour 26-00 3eme etage
Bureau 317
LIP6 – Université Paris 6
4, place Jussieu
75005 Paris – France
Tél :
+33 1 44 27 70 28 |
 |
| Email: Jean-Charles.Faugere [at] inria.fr |
|
|
|
|
|
Research
Interests:
Polynomial System Solving, Software, Academic and industrial applications,
Cryptology, Algebraic Cryptanalysis, Complexity analysis.
Keywords:
Gröbner Bases - Fast implementation - Computer algebra - Certified results - Efficient
software, Algebraic Cryptanalysis.
Polynomial System
Solving and Gröbner Bases ?
The notion of vector space is the dedicated mathematical
object when solving linear systems. Similarly the fundamental
mathematical object associated to a polynomial system of multivariate
equations is the ideal generated by the equations. From an
algorithmic point of view the main tool to represent an ideal is a
Gröbner basis (Bruno Buchberger). A Gröbner basis is a finite set of
polynomials which has desirable algorithmic properties. The historical algorithm to compute Gröbner bases is the Buchberger algoritm; more efficient algorithms (FGLM, F4, F5, fast FGLM) have been proposed to compute Gröbner bases more efficiently. A new trend in the field is to propose dedicated tool to solve structured polynomial systems (for using the symmetries induced by a finite group or the bilinear structure or determinantal ideals). Dedicated methods for finite fields have also been proposed. In practice, FGb is a fast library for computing Grobner Bases that can be used from Maple or from any C program. |
|
Gröbner
bases and Cryptography Last
years a new kind of cryptanalysis has made its entrance in
cryptography: the so-called algebraic
cryptanalysis. In a nutshell,
the idea of algebraic cryptanalysis is that for a given cryptosystem
one has to generate a suitable algebraic system of equations whose
zeroes correspond to the deciphered message or the secret key. A
fundamental issue of this cryptanalysis consists thus in finding
zeroes of algebraic systems. Gröbner bases, which are a fundamental
tool of commutative algebra, constitute the most elegant and
efficient way for solving this problem. They provide an algorithmic
solution for solving several problems related to algebraic systems.
From a practical point of view, we employed a fast Gröbner basis
algorithm, namely F5, for solving the corresponding algebraic system.
Very often this approach is efficient in practice and obliges to
modify the parameter of the cryptosystem. Some research papers FJ03, AFIK04, AF05, FP06a, FP06b, FLP08, FOPT10, FS10, FMR10, BFFP11, BFP11, AFFP11, FPPR12, BFP12. |
|
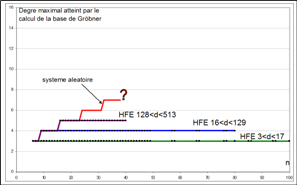
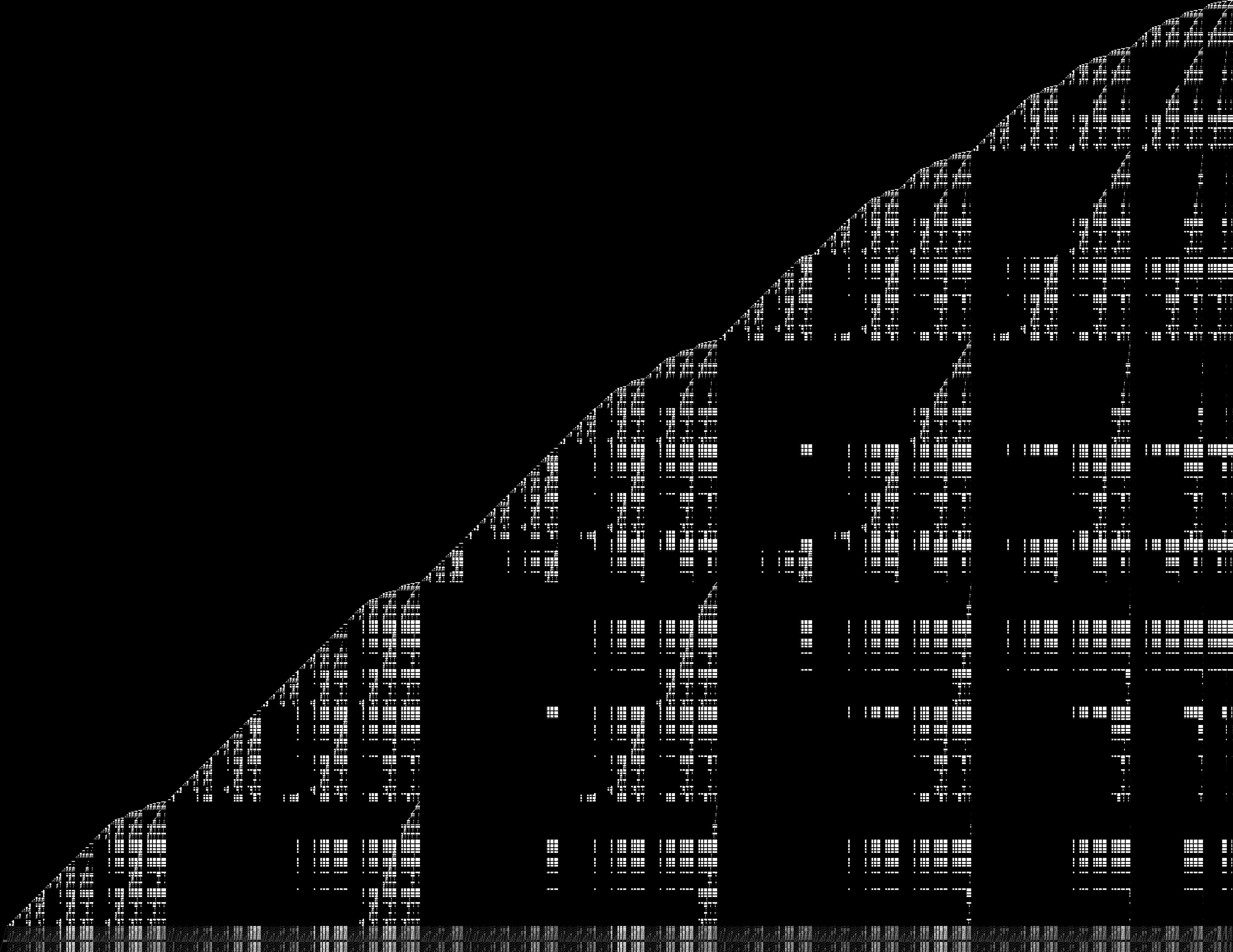
Understanding the complexity of computing Gröbner
bases is a fundamental issue. Following step by step the F5 algorithm it is possible to predict quite accurately the complexity of the computation. To this end, it is necessary to understand the shape of the matrices generated by F5 (generic quadratic system of 12 equations in 12 variables) [BFS2014]: |
|
|
|
|