How to call FGb from C Code ?

1. Download the library and the examples (updated version July, 2015) for Mac OS (Lion, intel 64) or Linux (Intel 64) (there is only one file for both Mac and Linux).

   The following text is just a short introduction to the full C interface documentation

2. Download and install the library: tar xvfz call_FGb6.maclinux.x64.tar.gz
   

cd <...>/call_FGb/nv/maple/C

1. Preliminary step:
   # a) gmp.h must be part of the compilation paths
   # if not you must copy it:
   cp <....>/gmp.h ../../nv/int
   # (for instance: cp ~/nv/int/gmp/i686/gmp/gmp.h ../../nv/int)
   # b) The gmp library must be available for the last step (link)
   # edit the file Makefile and modify the line: GMP_STATIC_DIR:=/home/jcf/nv/gmp/i686/gmp/.libs (or /home2/jcf/nv/gmp/darwin/gmp/.libs )

2. in the file Makefile adjust the variable
   
   LIBDIR := macosx
   
   or
   
   LIBDIR := x64
   
   

3. Compilation
   # You can can compile the demo program: several Groebner bases computations over a prime field or over the integers.
   # edit the files bug_multi.c bug_multi_modp.c and bug_multi_int.c : some comments can be uselful.
   #
   make

4. Run the program to compute a Groebner basis over Q (the result is quite big) and modulo a small prime. A NormalForm is also computed.

# ./main 1
Version FGb/int 9099 FGb/modp:9098
--------------------------------------------------
-------------------- STEP 0 -------------------
--------------------------------------------------
****************************** Compute gbasis over Q
INCREASE HEAP 1440096
Set offset primes to 0/20000
INCREASE HEAP 28941504
Lin Bk ignored [NEW lib]/S:0 -> 13/[2](2x4)COMPACT_NEW_LINES=1 BACKWARD=1
100%/[3](19x41)100%/[4](60x98)100%/[3](37x51)100%/[4](108x113)84.4%/100%/[3](75x71)100%/[4](85x86)100%/[5](106x115)100%/

Mingbasis2
(22x38)76.2%/100%/restore Z1 Copy 98.18 for 108/110 exposants
{38.10 per completed}
SWAP Z1/2 Memory usage (estimate): 0.000
/S:1 -> 26/
Mingbasis2
restore Z1 Compute_upper bound 10
{42.86 per completed}
SWAP Z1/2 Memory usage (estimate): 0.000
/S:2 -> 52/
Mingbasis2
restore Z1 Compute_upper bound 23
{done}
SWAP Z1/2 Memory usage (estimate): 0.000
21 polys in gbasis
[
75587301913761626619688784525326217114774228406208834864497695332705566102364711725545671591928961634536555282432000

*x6^4+
...
,1345843345732227321315104648533848883200*x5^2+1345843345732227321315104648533848883200*x6^2
+-208655494151930949482675216175654825559*1]
****************************** Compute NF
Set offset primes to 0/20000
Lin Bk ignored [NEW lib]/S:0 -> 13/
#C Second step time 0.00 sec
restore Z1 Copy 100.00 for 10/10 exposants
{done}
SWAP Z1/2 Memory usage (estimate): 0.000
2 pseudo normalForm have been computed
[
(1*x3*x4*x5+-1*x2*x4*x6)/1,(18*x4*x5+-9*x5^2+-18*x4*x6+9*x6^2+-10*x2+10*x3)/1]
****************************** Compute gbasis mod p
INCREASE HEAP 1440096
INCREASE HEAP 1808928
[2](10x21)COMPACT_NEW_LINES=1 BACKWARD=1
100%/{0,2,0,0}[3](34x46)100%/{0,2,4,0}[4](56x64)100%/{0,2,4,3}[5](53x60)100%/{0,2,4,3}[6](44x56)100%/{0,2,4,3}
Mingbasis2
(15x31)100%/[
1*x5^5+33257*x5^4+15685*x2*x5^2+2681*x3*x5^2+38871*x4*x5^2+41401*x5^3+8963*x2*x4+8833*x4^2+21302*x2*x5+
1710*x3*x5+11473*x4*x5+26979*x5^2+53967*x2+25106*x3+15783*x4+27238*x5,1*x2*x5^3+42001*x5^4+15451*x2*x5^2
+15414*x3*x5^2+49703*x4*x5^2+49856*x5^3+61132*x2*x4+3375*x4^2+7111*x2*x5+29175*x3*x5+64111*x4*x5+63391*x5^2
+50818*x2+41281*x3+49678*x4+25162*x5,
...
,1*x3*x4+58242*x4^2+1*x2*x5+50963*x3*x5+21844*x4*x5+21843*x5^2+3640*x2
+14560*x3+32760*x4+58240*x5,1*x1+2*x2+2*x3+2*x4+2*x5+65520*1]

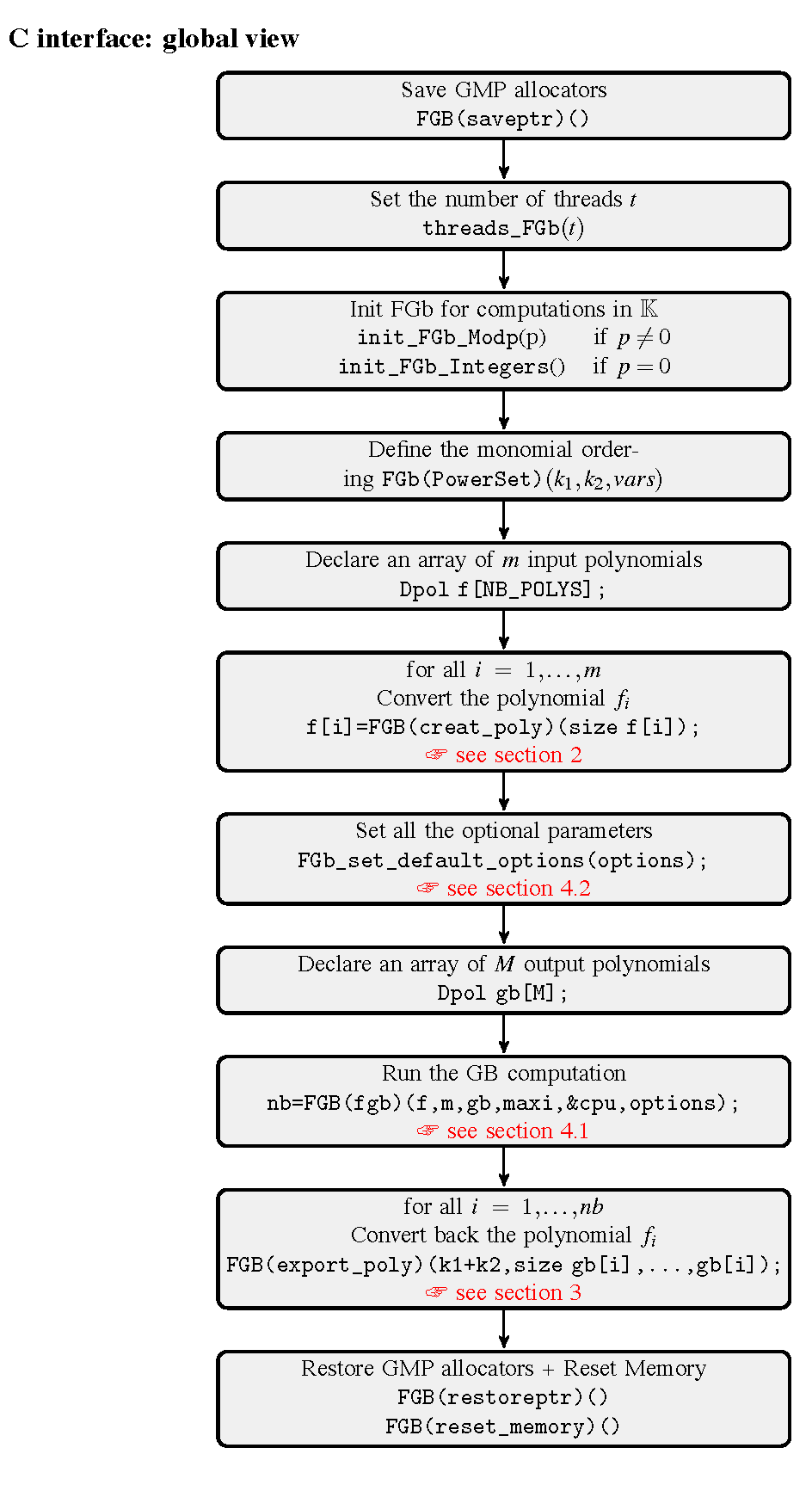
Example code: create a polynomial ring in FGb: