Goal and architecture of the FGb library
The purpose of the FGb library (206 052 lines of C) is twofold. First of all, the main goal is to provide efficient implementations of state-of-the-art algorithms for computing Gröbner bases: actually, from a research point of view, it is mandatory to have such an implementation to demonstrate the practical efficiency of new algorithms. Secondly, in conjunction with other software, the FGb library has been used in various applications (Robotic, Signal Theory, Biology, Computational Geometry, . . . ) and more recently to a wide range of problems in Cryptology (for instance, FGb was explicitly used in [2, 8, 9, 4, 5]
to break several cryptosystems).
Historically, the Gb library (191 420 lines of C++ code) has first been written to implement "classical" algorithms (Buchberger’s algorithm[1],
FGLM [12], NormalForms, Hilbert functions, . . . ). The current iteration of the project– the FGb library (206 052 lines of C code) – was restarted from scratch to demonstrate the practical efficiency of a family of new algorithms (F4[10], matrix-F5[6], F5[11], SAGBI-F5[6],. . . ). All these algorithms have in common that they rely heavily on linear algebra. Hence, whereas efficient internal representation for distributed multivariate polynomials was a key component in Gb, the critical part in FGb is the linear algebra package. The design of the library is somewhat modular: for instance, it is easy to add a
new field of coefficients K (FGb provides already 19 different fields); it is even possible to replace the existing linear algebra package by another one (see section section 4). Even if a small portion of the code has been written in assembler code the library is portable; to date the library is available on several architectures: Linux (64 bits), Mac (Intel 64 bits).
FGb has been used in many applications in crypology to break cryptosystems but also in mathematics, physics, engeneering science: some papers referring to FGb can be found here.
If you use FGb in a paper, we recommend you to follow this intructions to cite FGb.
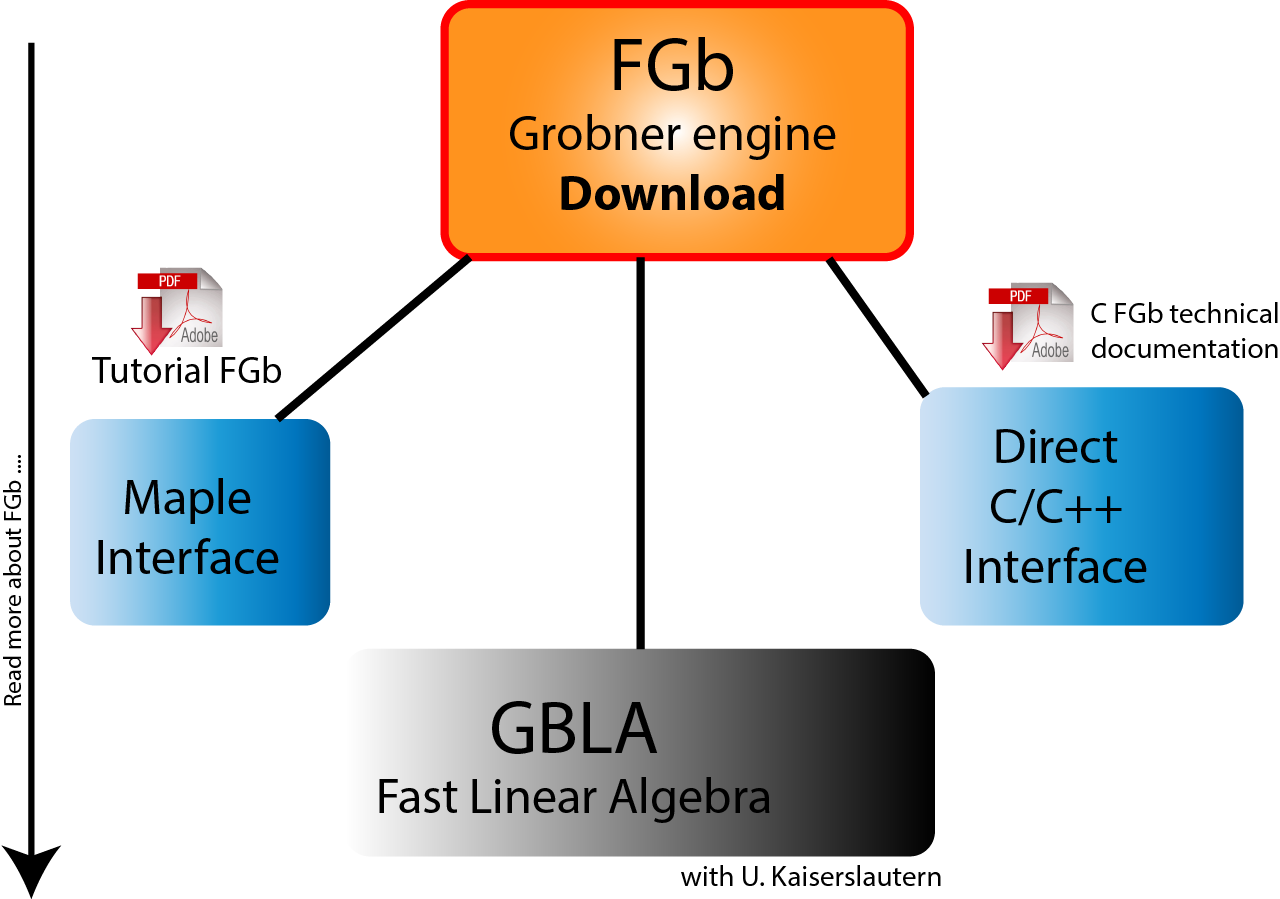
FGb can be used through three interfaces: Maple (shiped with recent versions of Maple), Maple/FGb (use my own package), from any C Code.
|
|
(B. Boyer, C. Eder, JC Faugere)
GBLA is an open source C library for linear algebra specialized for eliminating matrices generated during Gröbner basis computations in algorithms like F4 or F5.
Matrix database
Matrix database of large matrices in two formats. The newer format matrices are suffixed by .gbm and are prefered for downloading since they are an order of magnitude smaller in disk space.
Both formats are usable in GBLA (don't forget the -n option for using the newer format). The newer format produces much lighter matrices; we list the other format for legacy reasons.
Browse the Matrix Database (currently: 255 matrices, 71 Gb of downloads).
Benchmarks / Structured systems
Some benchmarks involving structured polynomial systems. |